São sete pontes e ficam num dos lagos do Jardim Mário Soares, no Campo Grande – mais para o lado de Entrecampos. São sete pontes que encerram em si um problema matemático – o das Sete Pontes de Königsberg, que foi resolvido por Leonhard Euler em 1736, mas que na próxima vez que passares por este espaço verde podes tentar resolver…
O problema das Sete Pontes de Königsberg surgiu há muitos anos atrás numa pequena cidade no norte da Europa, Königsberg, actualmente conhecida como Kaliningrad e que pertencia na altura à Prússia – hoje, Rússia. Königsberg era atravessada pelo Rio Prególia e tinha sete pontes, que permitiam atravessar de uma margem para a outra e chegar às duas ilhas que existiam no meio do curso de água: seis dessas pontes ligavam as ilhas às margens do rio e uma sétima ponte fazia a ligação entre as duas ilhas. Os moradores de Königsberg lançaram-se, a certo ponto, a um desafio: seria possível fazer um trajecto a pé de forma a passar uma única vez por cada uma das sete pontes e regressar ao ponto de partida?
Leonhard Euler, matemático, resolveu o problema em 1736, concluindo ser impossível. Mas esta questão da população de Königsberg acabou por levar Euler a criar a Teoria dos Grafos, que é actualmente uma das áreas mais importantes da matemática discreta. Um grafo é o modelo matemático ideal para o estudo das relações entre objectos discretos de qualquer tipo. É formado por vértices e por arestas. Usualmente, um grafo simples é representado por um diagrama no qual os vértices são representados por pontos e as arestas por linhas que unem vértices adjacentes.
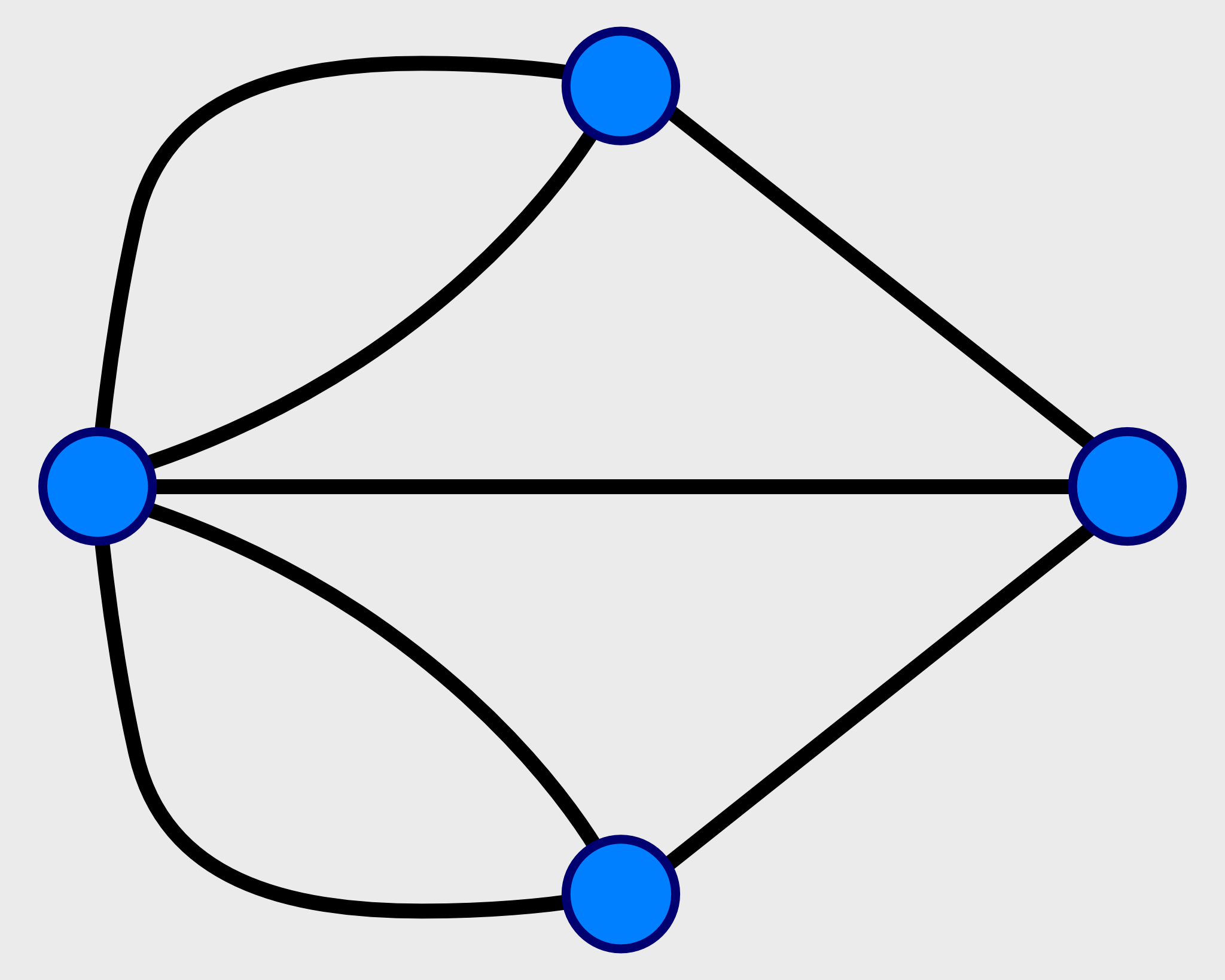
No caso do problema das pontes, o Euler concebeu um grafo com quatro vértices (pontos) – dois deles representando as duas margens do rio e os outros dois cada uma das duas ilhas – e com sete arestas (linhas) – uma aresta por cada ponte. Desta forma, Euler conseguiu reduzir o problema ao essencial eliminando as questões acessórias como o comprimento das pontes ou o tamanho das ilhas, focando-se apenas em desenhar um percurso que partisse de um dos quatro vértices e percorresse uma vez as sete arestas.
Ora, para passar por um vértice, são precisas duas arestas, uma para chegar ao vértice e outra para sair dele. Por isso, se para atravessar cada vértice são precisas duas arestas, é preciso que o número de arestas seja par, o que não acontece com o grafo das pontes. Apesar de o problema matemático das Sete Pontes de Königsberg ter tido como solução a impossibilidade da teoria proposta, Euler mostrou com ele que é possível usar os grafos para resolver problemas semelhantes noutra cidade e com um número diferente de pontes e de ligações.