There are seven bridges and they are located in one of the lakes of the Mário Soares Garden, in Campo Grande - more towards Entrecampos. They are seven bridges that contain within them a mathematical problem - that of the Seven Bridges of KönigsbergIt was solved by Leonhard Euler in 1736, but the next time you pass by this green space you can try to solve it...
The problem of Seven Bridges of Königsberg arose many years ago in a small town in northern Europe, Königsberg, now known as Kaliningrad, which belonged at that time to Prussia - today, Russia. Königsberg was crossed by the Pregolian River and had seven bridges, which made it possible to cross from one bank to the other and reach the two islands that existed in the middle of the watercourse: six of these bridges connected the islands to the banks of the river and a seventh bridge connected the two islands. The residents of Königsberg at one point set themselves a challenge: would it be possible to make a journey on foot so as to pass each of the seven bridges only once and return to the starting point?
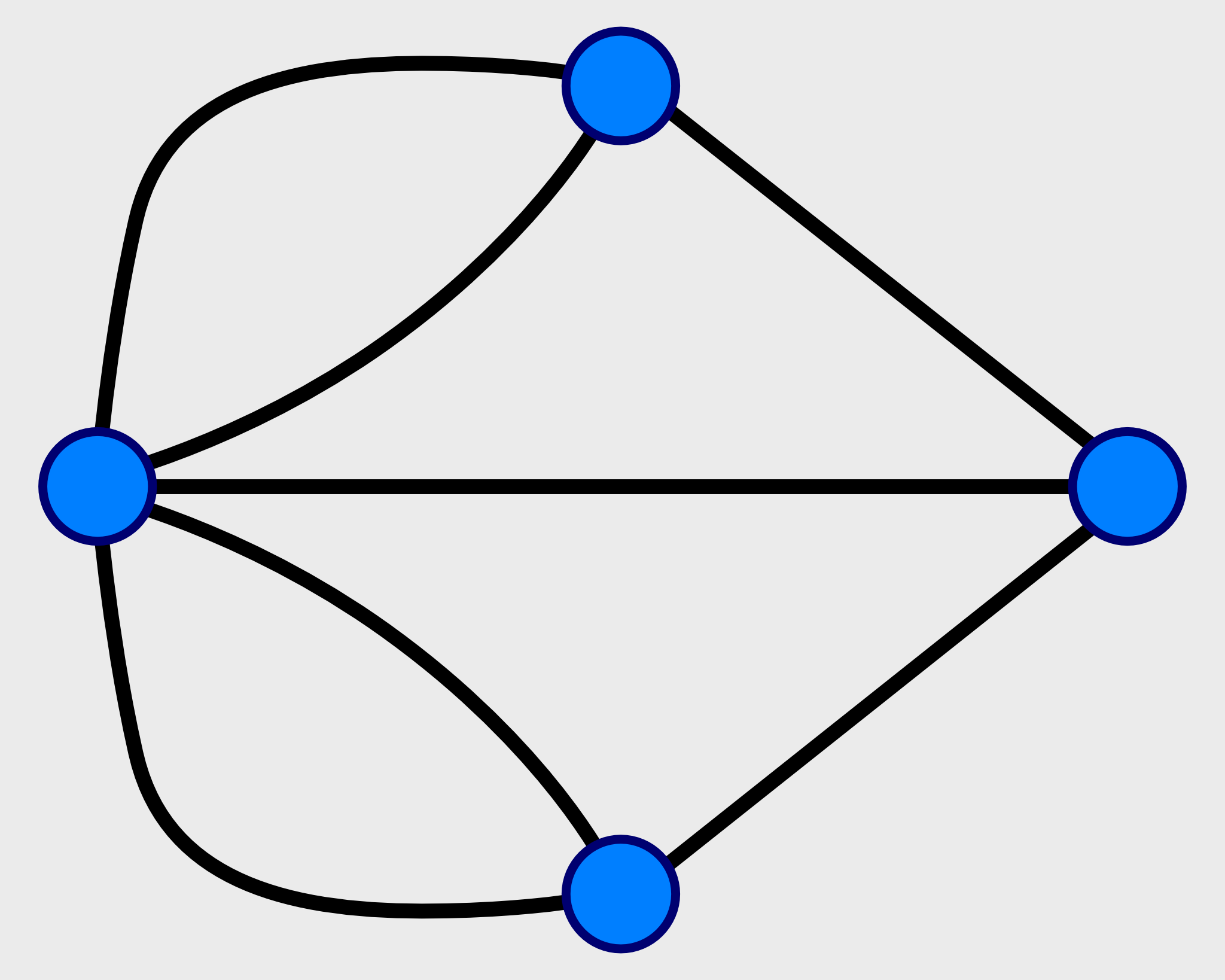
Leonhard Euler, a mathematician, solved the problem in 1736, concluding that it was impossible. But this question of the population of Königsberg eventually led Euler to create the Graph Theorywhich is currently one of the most important areas of discrete mathematics. A graph is the ideal mathematical model for studying the relationships between discrete objects of any type. It consists of vertices and edges. Usually, a simple graph is represented by a diagram in which vertices are represented by points and edges by lines connecting adjacent vertices.
In the case of the bridge problem, Euler designed a graph with four vertices (points) - two of them representing the two banks of the river and the other two each of the two islands - and with seven edges (lines) - one edge for each bridge. In this way, Euler was able to reduce the problem to the essentials by eliminating ancillary issues such as the length of bridges or the size of islands, focusing only on designing a path that started from one of the four vertices and traversed all seven edges once.
Now, to pass through a vertex, you need two edges, one to get to the vertex and one to get out of it. So, if it takes two edges to go through each vertex, the number of edges must be even, which is not the case with the bridge graph. Although the mathematical problem of Seven Bridges of Königsberg having had as a solution the impossibility of the proposed theory, Euler showed with it that it is possible to use graphs to solve similar problems in another city and with a different number of bridges and links.